1. 숫자형 변수(양적 데이터)
카페 안 손님 20명의 나이 데이터(정보)가 있다고 하자. 이 데이터를 한눈에 파악하기 위해 무엇을 하면 좋을까?
이처럼 숫자형 변수를 정리하는 방법에는 두 가지가 있다.
1-1) 기초통계량: 숫자(정보의 대푯값)로 요약하는 describe()
어떤 데이터를 하나의 숫자로 요약하면 뭐야? 한두 개의 숫자로 요약해봐. 했을 때 그 숫자가 대푯값이다. 숫자형 변수를 한눈에 파악하기 위해서는 이러한 대푯값으로 요약하는 방법이 있다.
(1) 평균(mean)
우리는 보통 산술평균을 사용하고 있지만, 평균에는 산술 평균, 기하 평균, 조화 평균 등 다양한 종류가 있다. 어떤 평균을 활용할지 잘 검토하여 선택하자.
# 넘파이 함수 이용하기- 넘파이 어레이로 변화시켜서 계산. 시리즈, 리스트 가능
np.mean(titanic['Fare'])
# 판다스의 mean 메서드 이용하기- 시리즈에 딸려 있는 메소드
titanic['Fare'].mean()
[참고] 평균을 대푯값으로 사용할 때 주의할 점
도서관 회원과 대출을 분석할 때, 회원의 평균 나이가 23.5세라고 한다. 회원들은 어떤 사람들일까?
- 학생들? 대학생? 취업준비생들?

(2) 중위수(median)
자료의 순서상 가운데 위치한 값을 말한다.
# 넘파이 함수 이용하기
np.median(titanic['Fare']) # 14.45 달러 내고 가운데 위치한 사람이 탔나보다
# 판다스의 median 메서드 이용하기
titanic['Fare'].median() # 위와 동일한 결과
(3) 최빈값(mode)
자료 중에서 가장 빈번한 값을 말한다.
# 판다스의 mode 메서드 이용하기
titanic['Pclass'].mode() # 가장 빈도가 높은 게 3등급임을 알 수 있다.
# 좌석등급별로 수를 살펴보자.
titanic['Pclass'].value_counts()
(4) 사분위수(quartile)
데이터를 4등분해서 각 구간의 경계값을 알려주는 값이다. 중앙값(2사분위수)를 포함해 총 4개의 구간으로 나누어주며, 이를 통해 데이터의 분포를 쉽게 파악할 수 있다.
titanic['Fare'].describe()
1-2) 기초통계량의 시각화: plt.boxplot() / sns.boxplot()
matplotlib을 사용한 plt.boxplot()을 사용할 때에는 사전에 반드시 NaN 값을 지워줘야 그래프를 그릴 수 있다.
- vert 옵션: 세로(True, 기본값), 가로(False)


# titanic['Age']에는 NaN이 있습니다. 이를 제외한 데이터
temp = titanic.loc[titanic['Age'].notnull()]
plt.boxplot(temp['Age'])
plt.grid()
plt.show()
# 옆으로 그리기
plt.boxplot(temp['Age'], vert = False)
plt.grid()
plt.show()
seaborn 패키지 함수들은 NaN을 알아서 빼고 그려준다.
# 가로로 그리려면 X에 설정
sns.boxplot(x = titanic['Age'])
plt.grid()
plt.show()
# 세로로 그리려면 Y로 설정
sns.boxplot(y = titanic['Age'])
plt.grid()
plt.show()
2-1) 도수분포표: cut()/qcut()과 value_counts()를 통한 구간별 빈도수
숫자형 변수를 정리하는 다른 방법은 구간을 나누고 빈도 수(frequency)를 계산하는 것이다. 이를 정리한 표를 도수분포표라고 한다. 이를 위해서는 앞서 다루었던 cut(), qcut()으로 먼저 구간을 나눈 뒤에, value_counts()를 통해 구간별 빈도수를 계산해줄 수 있다.
# 5개의 구간으로 나누기
bins = [0, 20, 40, 60, 80, 100]
labels = ['0-20', '21-40', '41-60', '61-80', '81-100']
# 구간으로 나누기
categories = pd.cut(data, bins=bins, labels=labels, right=True)
# 구간별 빈도수 계산
frequency = categories.value_counts()
2-2) 도수분포표의 시각화: Histogram과 Density plot(KDE)
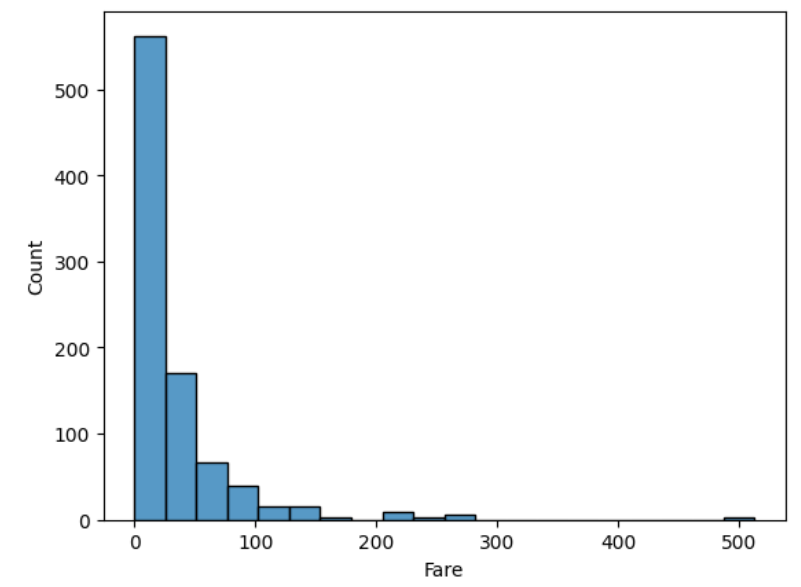
각 구간마다 얼마나 데이터가 있는지는 히스토그램을 통해 시각화해볼 수 있다.
plt.hist(titanic.Fare, bins = 30, edgecolor = 'gray')
plt.xlabel('Fare')
plt.ylabel('Frequency')
plt.show()
# seaborn 활용
sns.histplot(x= 'Fare', data = titanic, bins = 20)
plt.show()
그러나 '어디에 쏠려 있네', '위로 솟아있네'. 이러고 땡이 아니라, 그 안에 담겨 있는 이유를 찾아야 한다. 이때 기술적인 지식도 필요하지만, 비즈니스적 지식이 있어야 본격적으로 해석이 가능하다.
그래프 읽는 방법
1. 축의 의미를 파악해라. x축은 무엇을 의미하나? y축은 무엇을 의미하나?
2. 희박구간과 밀집 구간을 찾고, '왜 그 구간은 희박/밀집한지' 비즈니스적 의미를 찾아라.
그래프를 제대로 읽으려면,
① 먼저 축의 의미를 파악해야 한다. 축에 x축도 있고, y축도 있다.
축을 모르면 내용물은 볼 필요도 없다. 기준이 없는 것이다. 축은 우리가 내용을 보기 위한 기준점이고, 베이스이기 때문에 반드시 축을 이해해야 한다. x축의 의미가 뭐고 y축의 의미가 뭔지 살펴봐야 한다.
② 다음으로는 분포를 봐야 한다. 어디가 밀집되어있고, 어디가 희박한지를 찾는 것이다. (만약 판매량을 가지고 히스토그램을 그렸다. 봤더니 왼쪽으로, 오른쪽으로 치우쳐진 것을 봤다. 그러면 값이 높은 쪽에 밀집되어있구나. 하고 파악해볼 수 있다.) 이때, 밀집/희박한 데에는 반드시 그에 합당한 비즈니스적 의미가 있을 것이다. 통계량을 내고, '왜 그렇지' 하고 되물어보는 자세를 갖추는 게 중요하다.
이유를 정말 모르겠다면?
모를 수도 있다. 그러면 잘 알고 있는 사람에게 물어봐야 한다. 따라서 보통 데이터 분석을 하면 반드시 현직자에게 물어본다. 현장의 반장님들과 미팅도 하고, 어떻게 이 철로부터 철판이 만들어지는지 공정, 이런 것도 배우고 한다.
이처럼 왜 밀집되어있고 희박한지 알려면 현장의 도메인 전문가에게 물어봐야 한다. 매장에 가서 판매하는 것도 보고, 점장님들 이야기도 듣고. 현장에 가야 한다. 현장에 가는 게 굉장히 중요하다.
한편, 히스토그램은 단점이 하나 있다.
구간을 8개로 나눌 때, 64개로 나눌 때 보이는 것들이 다르다는 점이다. 구간의 개수에 따라서 파악할 수 있는 내용이 많이 달라지게 된다. 따라서 히스토그램을 그릴 때에는 bins를 적절히 조절하는 것이 관건이 된다.

이러한 단점을 해결하기 위해서 밀도 함수 그래프(KDE plot)을 사용한다. 이는 막대의 너비를 가정하지 않고 모든 점에서 데이터의 밀도를 추정하는 커널 밀도 추정(Kernel Density Estimation) 방식이다. 확률을 내가 가늠해볼 수 있도록 해주는 그래프라는 뜻이다.
이 그래프의 특징적인 부분이 있는데, 그래프의 아래 면적이 1이라는 점이다. 이러한 면적으로 구간에 대한 확률을 추정해볼 수가 있다.

sns.kdeplot(titanic['Fare'])
# sns.kdeplot(x='Fare', data = titanic)
plt.show()
3) 단변량 분석 함수 생성: 숫자형 변수
def num_ana(data, feature, bins = 30) :
print(data[[feature]].describe().T) # 기초통계량 및 분포 확인
print() # 공백
plt.figure(figsize = (10,4))
plt.subplot(1,2,1)
sns.histplot(x=data[feature], bins = 20, kde = True) # 히스토그램 출력
plt.subplot(1,2,2)
sns.boxplot(x=data[feature]) # 박스플롯 출력
plt.tight_layout()
plt.show()num_ana(data, 'Sales')
2. 범주형 변수(질적 데이터)
00초등학교 3학년 2반 학생들의 성별(범주)를 분석하려고 해보자. 이들의 성별을 어떻게 파악할 수 있을까?
간단하게 생각하면, 범주별 개수를 세면 될 것이다. 3학년 2반의 남학생들을 세고, 여학생들을 따로 세어서 범주별 빈도수와 범주별 비율을 구해볼 수 있을 것이다.
수치형 변수였을 때는 수집할 때 도구도 다양하고 했었지만, 범주형 변수일 때에는 굉장히 단순하다. 범주별 개수를 그냥 세버리면 된다.
1) 기초통계량: 범주별 빈도수 / 범주별 비율
범주별 빈도수는 value_counts()를 사용하는데, 범주별 비율은 그 안의 매개변수로 normalize=True를 설정해주어서 구해준다.
# 범주별 빈도수
titanic['Pclass'].value_counts()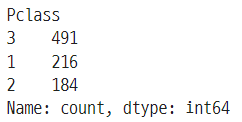
# 범주별 비율
titanic['Pclass'].value_counts(normalize = True)
2) 범주형 변수의 시각화: sns.countplot() / plt.pie()
sns.countplot()
범주별 빈도수는 value_counts()를 사용하는데, 범주별 비율은 그 안의 매개변수로 normalize=True를 설정해주어서 구해준다. plt.bar() 를 이용하려면 먼저 집계한 후 결과를 가지고 그래프를 그려야 하는데, countplot은 집계 + bar plot을 한꺼번에 해결해주기에 countplot()을 활용하도록 하자.
# sns.countplot(x=titanic['Pclass'])
plt.figure(figsize=(10,5))
plt.subplot(1, 2, 1)
sns.countplot(x='Pclass', data=titanic)
plt.subplot(1, 2, 2)
sns.countplot(y='Pclass', data=titanic)
plt.grid()
plt.show()
plt.pie()
범주별 비율을 비교할 때 파이차트를 사용하기도 한다. 역시 먼저 집계를 해주어야 하는데, 다음과 같이 표시한다.
- plt.pie( 값, labels=범주이름, autopct = ‘%.2f%%’)
- autopct는 그래프에 표시할 비율 값에 대한 설정이며, .2f는 소수점 두 자리 퍼센트로 표기함을 의미
temp = titanic['Pclass'].value_counts()
plt.pie(temp.values, labels = temp.index, autopct = '%.2f%%')
plt.show()
다음처럼 추가 옵션을 지정할 수도 있다.
각도와 방향 조정
- startangle = 90 : 90도 부터 시작
- counterclock = False : 시계 방향으로
plt.pie(temp.values, labels = temp.index, autopct = '%.2f%%',
startangle=90, counterclock=False)
plt.show()
간격 띄우고, 그림자 넣기
- explode = [0.05, 0.05,0.05] : 중심으로 부터 1,2,3 을 얼마만큼 띄울지
- shadow = True : 그림자 추가
plt.pie(temp.values, labels = temp.index, autopct = '%.2f%%',
startangle=90, counterclock=False,
explode = [0.05, 0.05, 0.05], shadow=True)
plt.show()
3) 단변량 분석 함수 생성: 범주형 변수
def cat_ana(data, feature) :
# 기초 통계량
print(f' <<< {var} >>') # 제목 출력
cnt = data[feature].value_counts() # (1) 범주별 개수
prop = data[feature].value_counts()/data.shape[0] # (2) 범주별 비율
temp = pd.DataFrame({'Class':cnt.index, 'Count':cnt.values, 'Prop':prop.values})
display(temp) # (1), (2)를 하나의 데이터프레임으로 생성해 출력
# 시각화
sns.countplot(x = feature, data = data)
plt.grid()
plt.show()feature = 'ShelveLoc'
cat_ana(data, feature)
'데이터 분석 > 비즈니스 데이터 분석' 카테고리의 다른 글
| 가설 검정(이변량 분석): 숫자-숫자 / 범주-숫자 / 범주-범주 / 숫자-범주 (1) | 2024.09.28 |
|---|---|
| 데이터 분석 방법론(CRISP-DM) (2) | 2024.09.27 |